Tanisha Pal Singh
13 March 2019
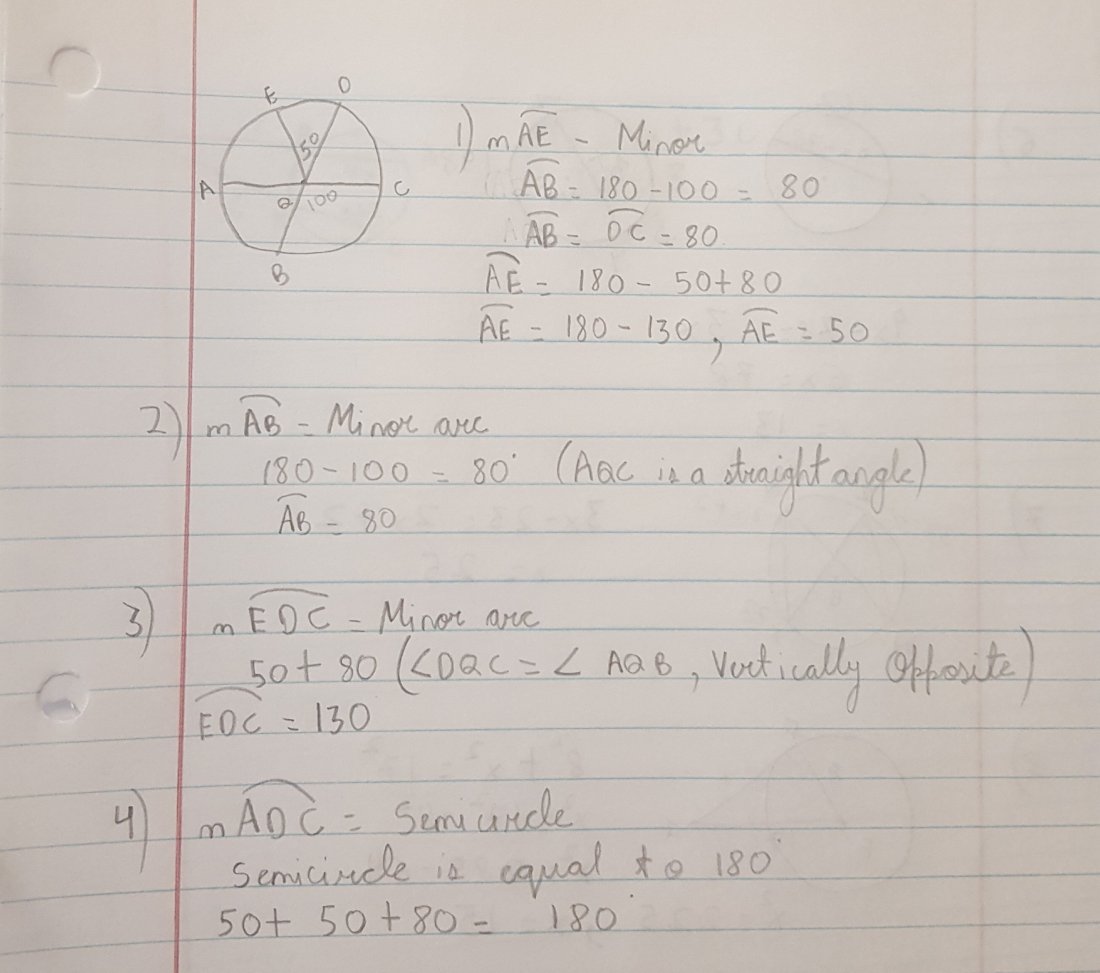
1) Arc AE is a minor arc because it is less than 180. We will find out it’s measure angle AQB by subtracting 100 from 180 as AQC is a linear pair. Angle AQB is 80. AQB and DQC are vertically opposite. So DQC is also 80. Now, we can find out AQE by first adding 50 and 80 which would give us 130 and then we will subtract that from 180. So AQE is 50 and Central angle is equal to its arc. So arc AE is 50.
2) AB is a minor arc because it’s measure is less than 180. We know that AQC is straight angle. So we can subtract 100 from 180 which is 80. AQB is equal to arc AB which is 80.
3) Arc EDC is also a minor arc as it is less than 180. We know DQC and AQB are vertically opposite. So DC is 80 and ED is 50. We will add those which is 130 which is arc EDC.
4) Arc ADC is a semicircle because it’s endpoint are on endpoints of diameter. Semicircle is always equal to 180 but we can find that by adding AQE, EQD and DQC. So 50+50+80 which is 180.
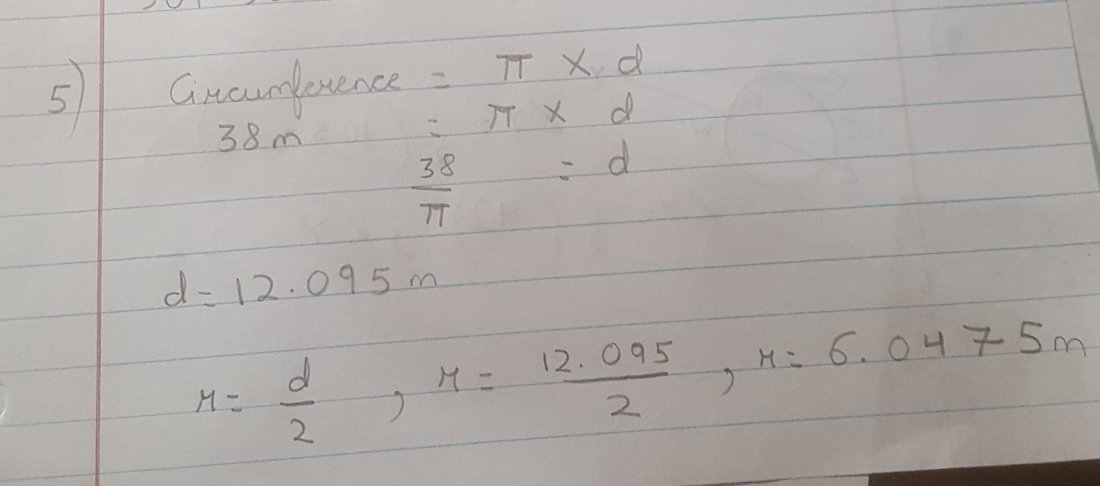
5) We have to find out diameter and radius. We know circu.ference is the product of pie and diameter. We will put the values in equation. So 38 m is equal to pie and diameter. Sister is equal to 38 divided by pie. So diameter would be 12.095 m. We know radius is the half of diameter. So we will divide 2 by 12.095 m which would give us the radius as 6.0475 m.
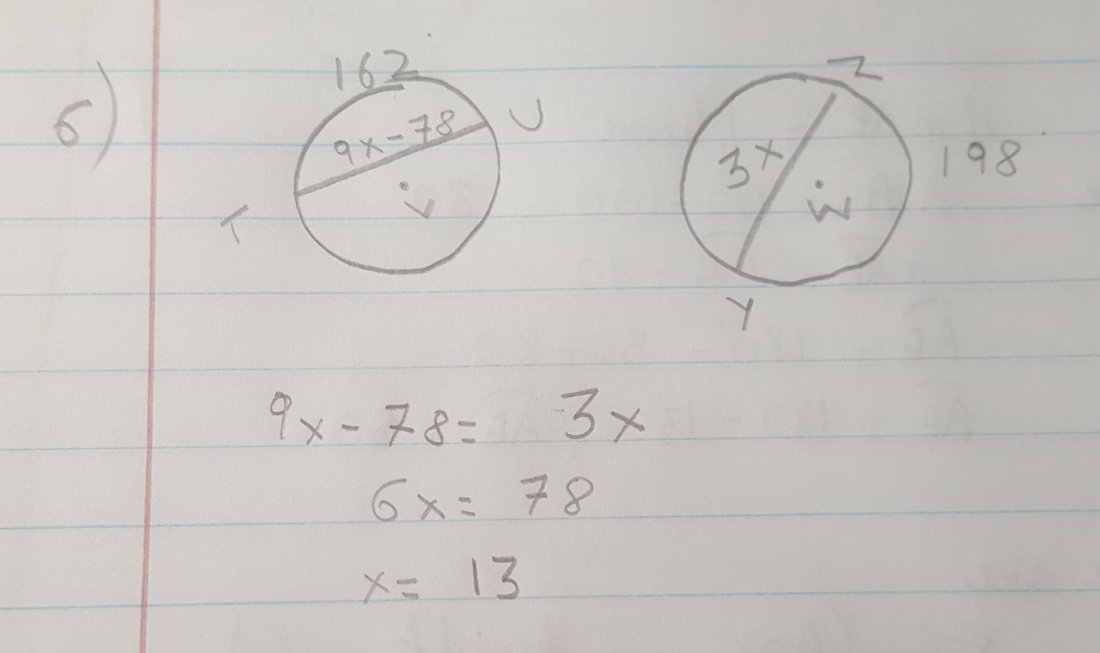
6) The circles are congruent to each other and arc are also congruent because 360- 162 is 198. So the chords are also congruent. We have to solve for x. We will set 9x-78 and 3x equal to each other. We will put variables on one side and numbers on other. So +3 would subtract on going on left side and -78 would become +78. So 6x is equal to 78. x is equal to 13.
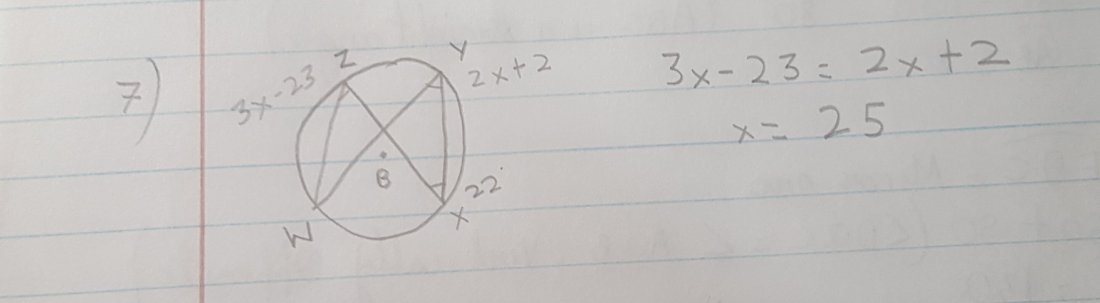
7) We know that if two Inscribed angles of a circle intercept the same arc or congruent arcs, then the angles are congruent. So we will set 3x-23 and 2x+2 equal to each other and solve for x. 2x would subtract on left side and -23 would add on right side. So x is equal to 25.
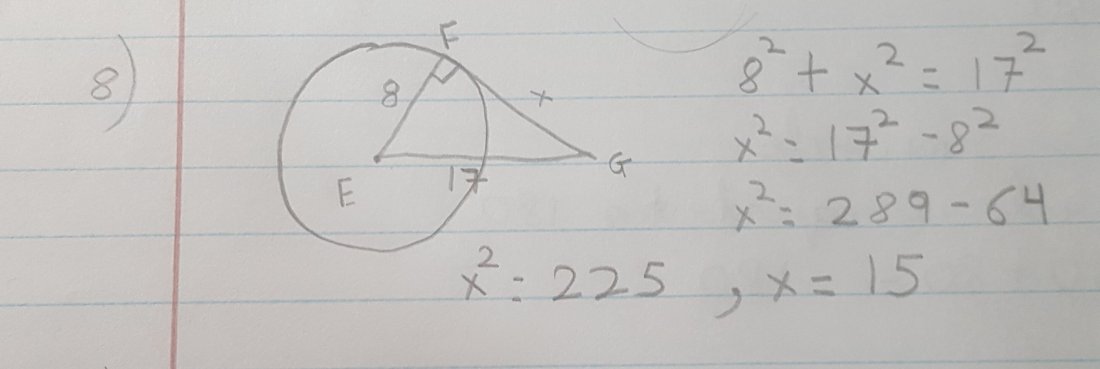
8) We have to solve for x. Where a radius meets a tangent it forms 90 degree. So 17 is hypotenuse. So 8^2 + x^2 = 17^2. So x^2 would be equal to 289- 64 which would be 225. We will do square root of 225 which would give us x as 15.
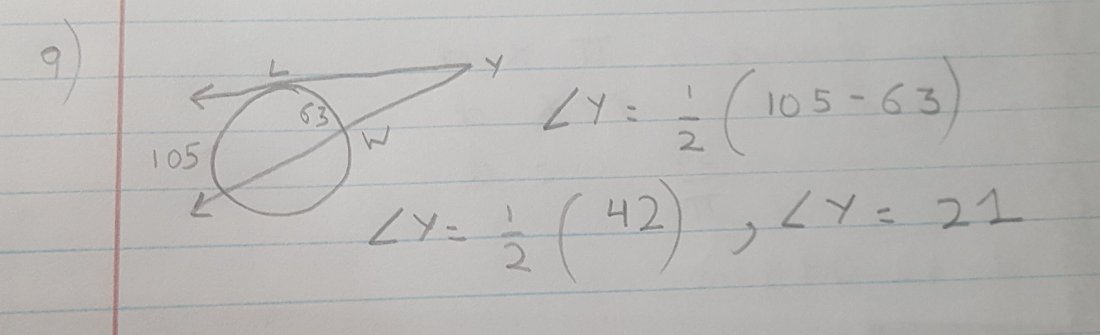
9) If two intersecting secants meet on the exterior of the circle, the angle formed by two secants outside is half the measure of big arc- small arc. So angle Y would be 1÷2 (105- 63), 1÷2 × 42. So angle Y would be 21.
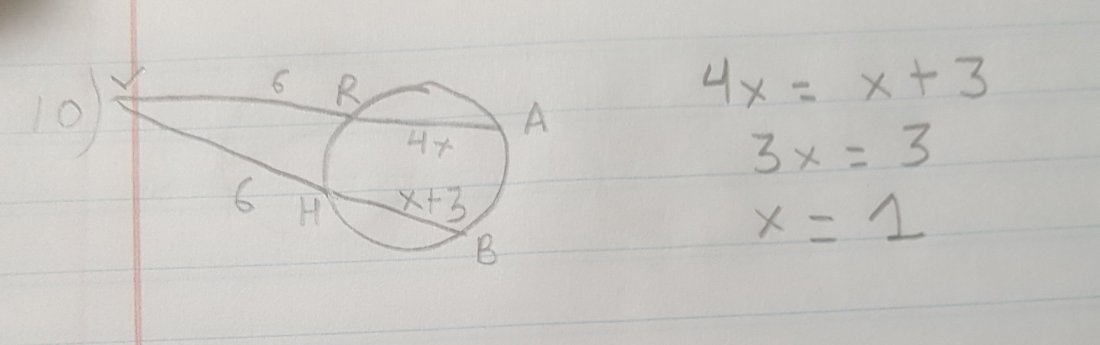
10) The outside of the circle is equal so we can set 4x and x+3 equal to each other. So 4x= x+3
3x= 3. x=1