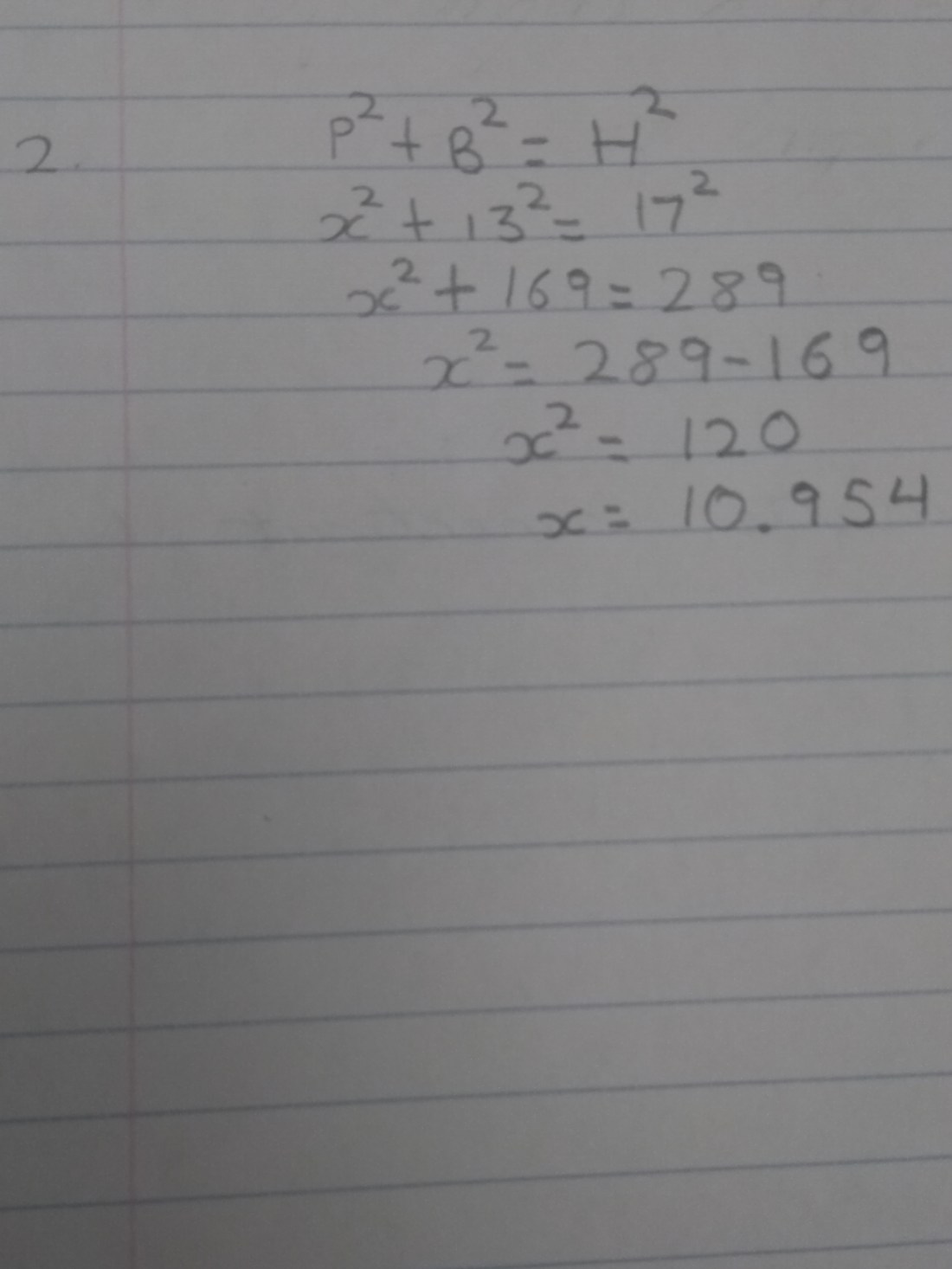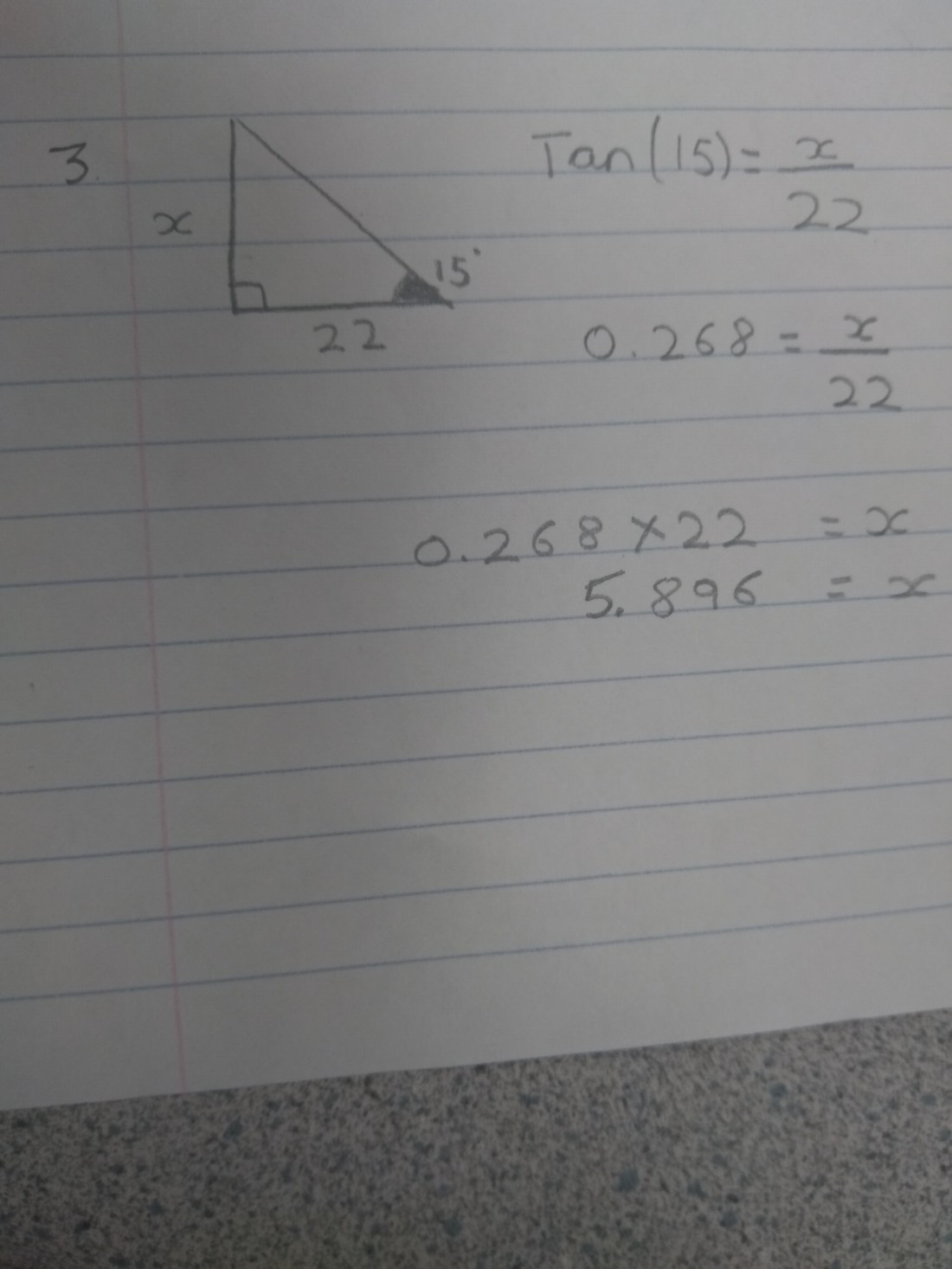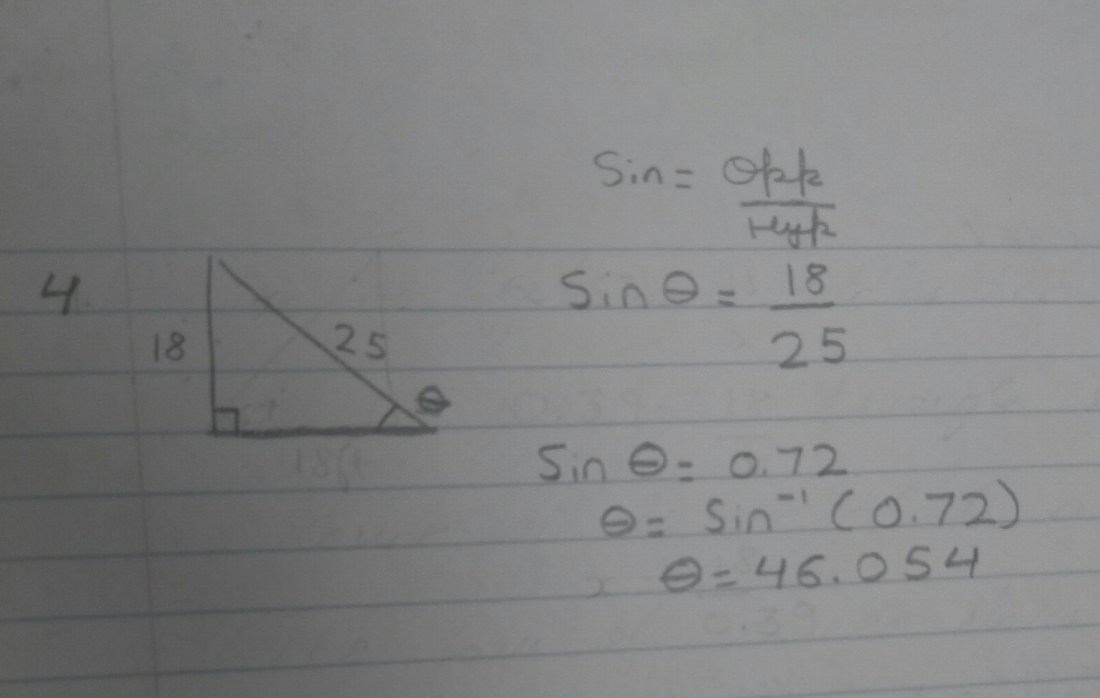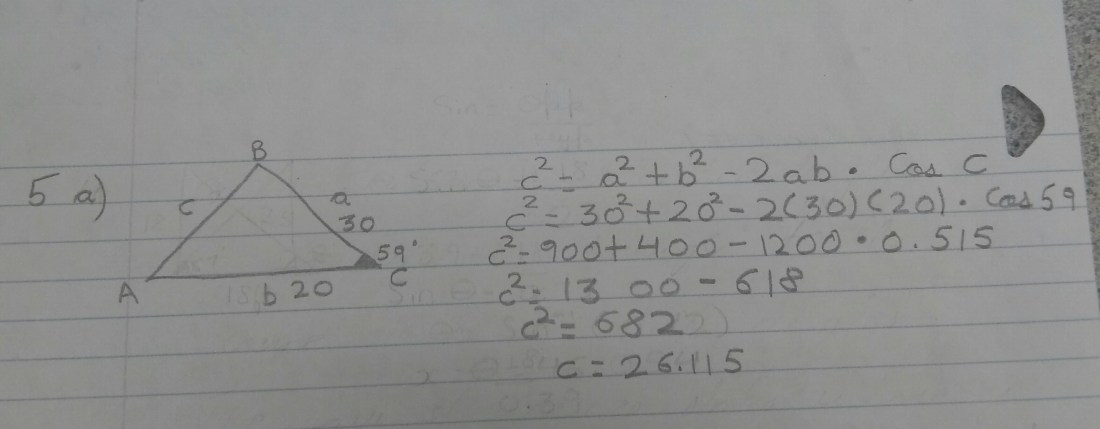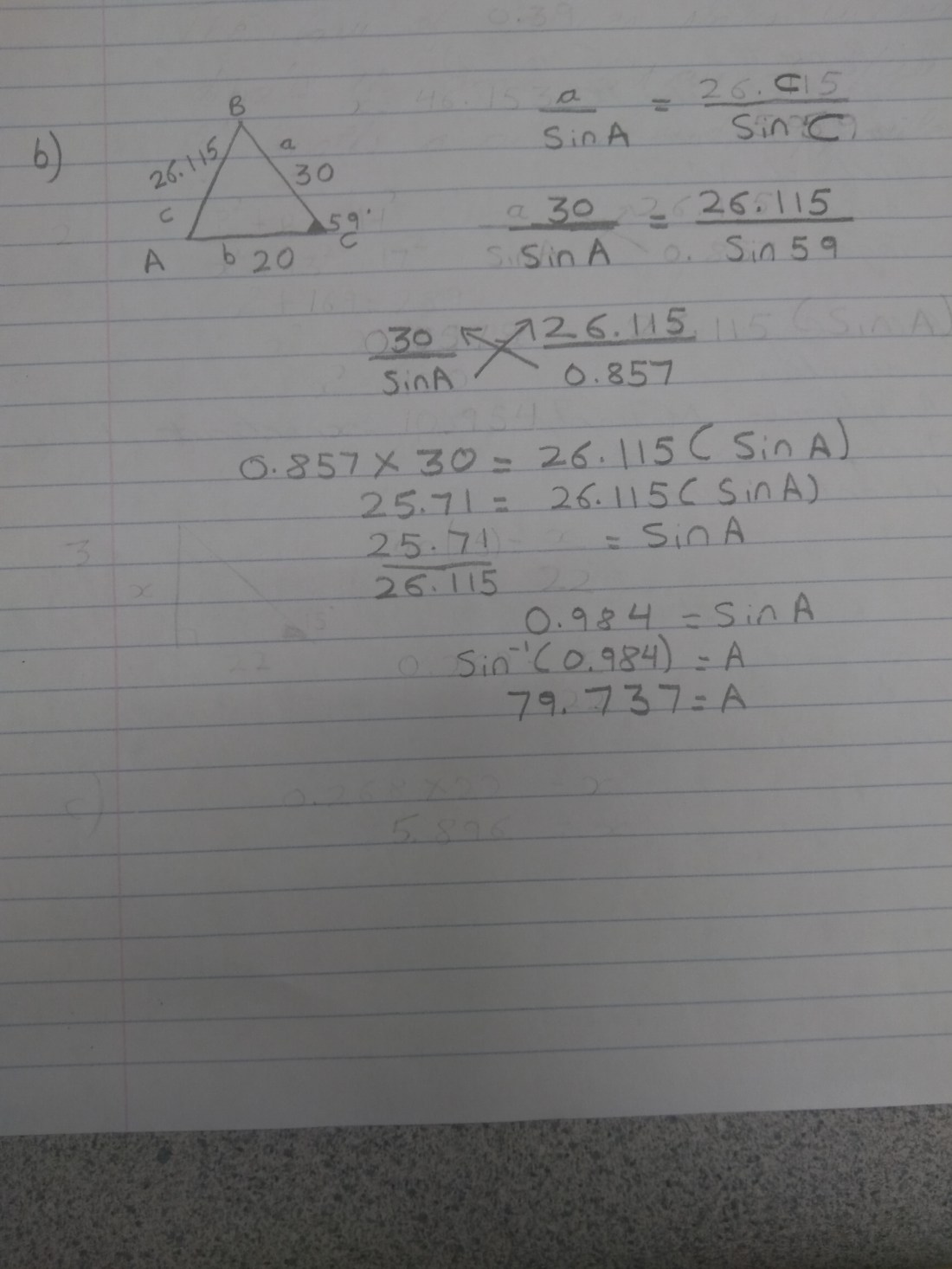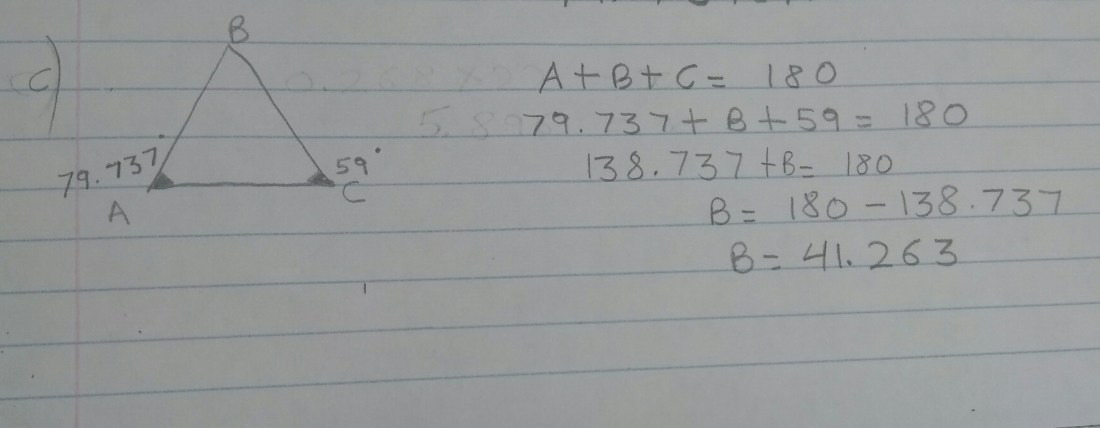Tanisha Pal Singh
10 December. ( Another response)
1)
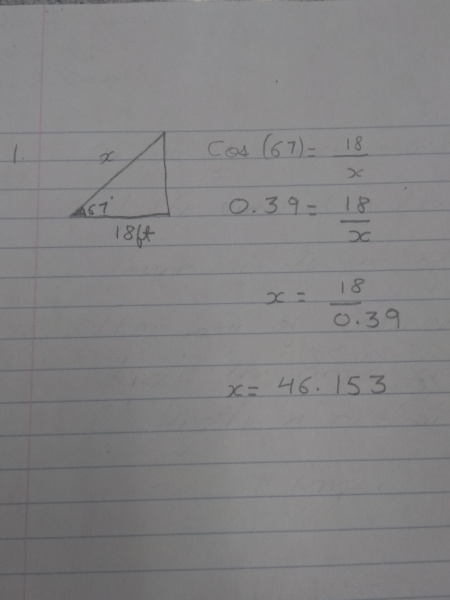
1) A ladder is leaning against the house which will be the hypotenuse. It forms 67 degree angle with the ground. The foot of the ladder is 18 feet away from the house which will make the base 18. We have to find the length of the ladder which will be the height. Now we have been given two values and we have to think of a formula which will put values in correct position and we will be able to find out x. The appropriate formula would be cos= adjacent ÷ hypotenuse. We will put values and we will solve. So cos 67 would be equal to 18÷ x. Then we would have to do cos 67 in our calculator, which would be 0.39 . 0.39 would be equal to 18÷ x. Now we have to find x. So x is equal to 18÷ 0.39 . x is equal to 46.153 .
2)

We have to find out x which is perpendicular and we have been given hypotenuse and base as 17 and 13 respectively. The formula is P^2 + B^2 = H^2 . Now we will plug it in. So P^2 + 13^2 = 17^2 . Now we will solve. So P^2 + 169= 289. P^2= 289- 169. P^2= 120. We are looking for P. So we will put in calculator square root of 120 which will come 10.954 and that will be our x.
3)

We have to find out x which is opposite and we have been given adjacent as 22 and we have been given theta as 15. Now we have to think of a formula which will put opposite and adjacent and theta in a formula. Tan is equal to opposite÷ adjacent. Now we will plug in values. So Tan 15 is equal to x divided by 22. Tan 15 we will put in calculator and it would be equal to 0.268 . Now 0.268 would be equal to x divided by 22. So x is equal to 0.268 multiplied by 22 and x will be equal to 5.896
4)

We have been given two sides and we have to find out theta. We have been given opposite and hypotenuse as 18 and 25 respectively. So we will use sin formula because sin is equal to opposite divided by hypotenuse. Now we will plug in. So theta is equal to 18 divided by 25. Theta is equal to 0.72 . x is equal to inverse of sin multiplied by 0.72 . Theta will be equal to 46.054
5 a)

We have been given angle C and sides a as 30 and b as 20. We have to find out side c. Law of cosines in this case will be c^2= a^2 + b^2 – 2ab × cos C
c^2= 30^2+ 20^2- 2 × 30 × 20× cos 59.
c^2 will be equal to 900 plus 400 minus 1200 multiplied by 0.515 . c^2 will be equal to 1300 minus 618 which will be equal to 682. We have to find out c, so we will put square root of 682 which will be equal to 26.115
5b)

We have to find out angle A using law of sines. We have side a, side c and angle C. So side a divided by sin A is equal to side c divided by angle C. We will plug in the values. 30 by sin A is equal to 26.115 by sin 59 which will be equal to 0.857 . Now we will cross multiply, so 0.857 multiplied by 30 is equal to 26. 115 multiplied by sin A . So sin A is equal to 25.71 divided by 26.115. Sin A is equal to 0.984 . A is equal to 79.737
5c)
 W have been given angle A and angle C as 79.737 and 59 respectively. A+ B + C is equal to 180. Every triangle is equal to 180 degree total. So now we will plug in, 79.737+ B+ 59= 180
W have been given angle A and angle C as 79.737 and 59 respectively. A+ B + C is equal to 180. Every triangle is equal to 180 degree total. So now we will plug in, 79.737+ B+ 59= 180
138.737+ B= 180
B will be equal to 180 minus 138.737. So Angle B will be equal to 41.263



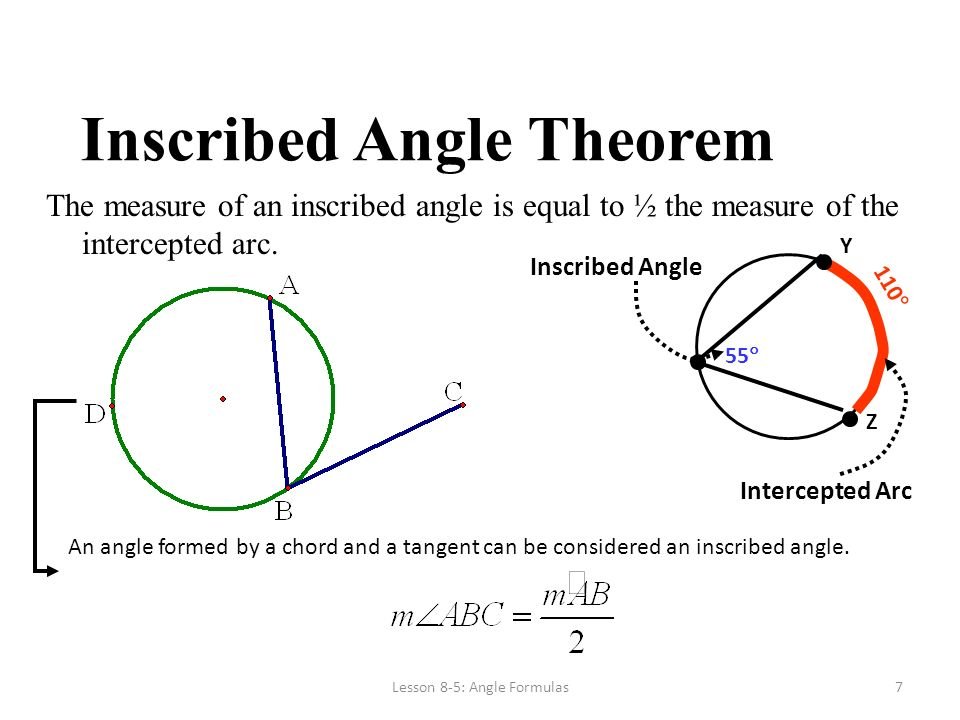
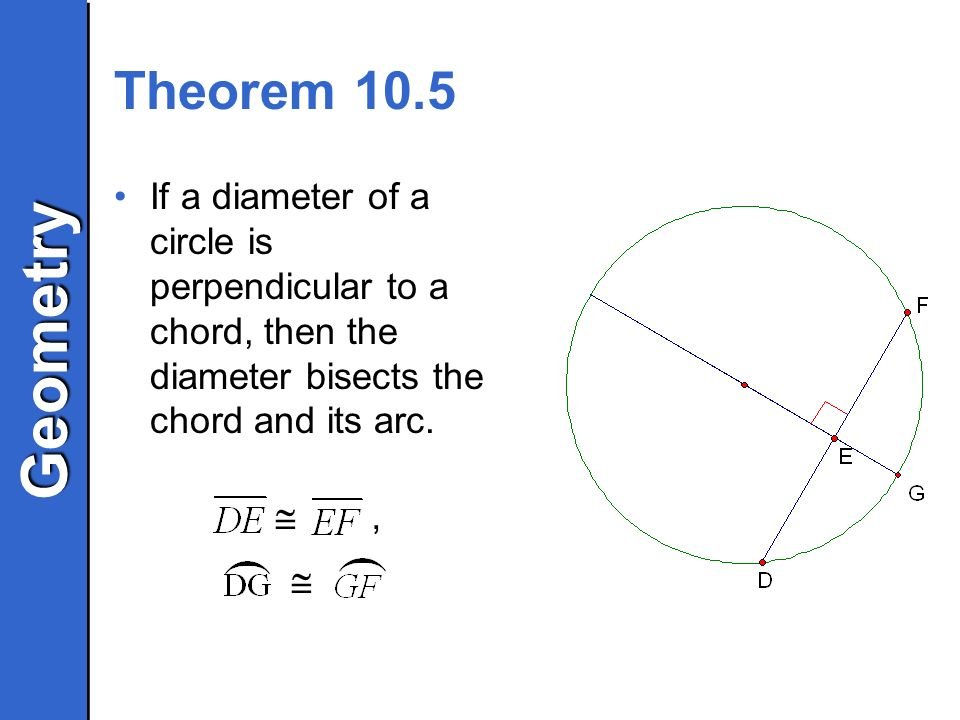

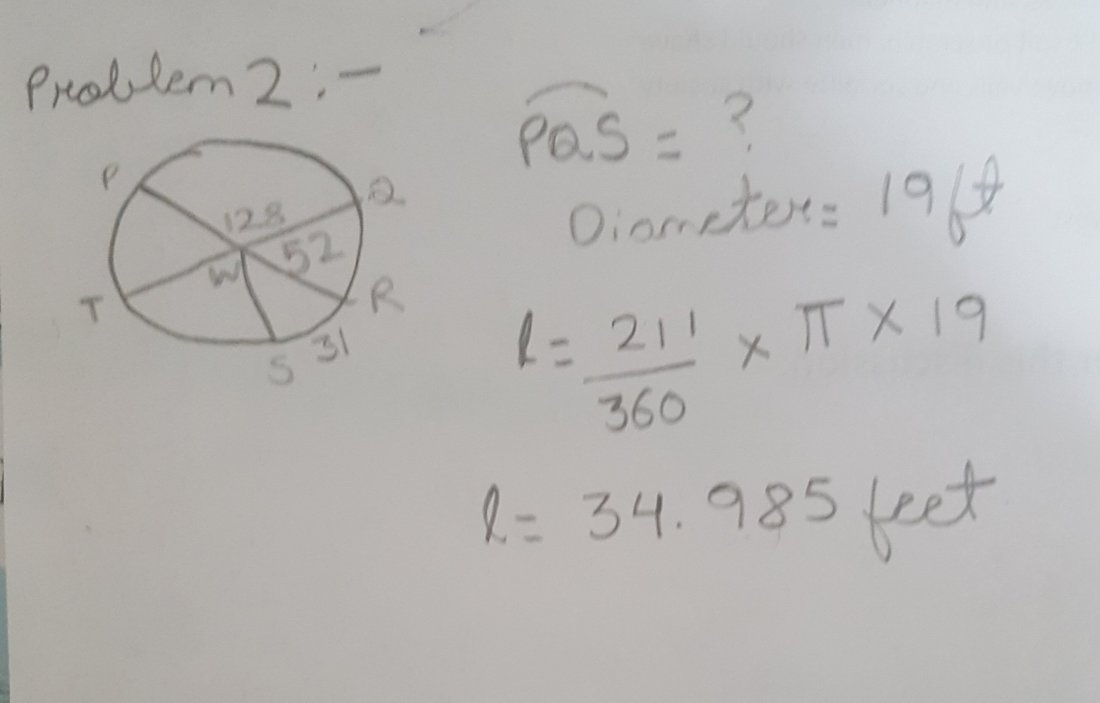
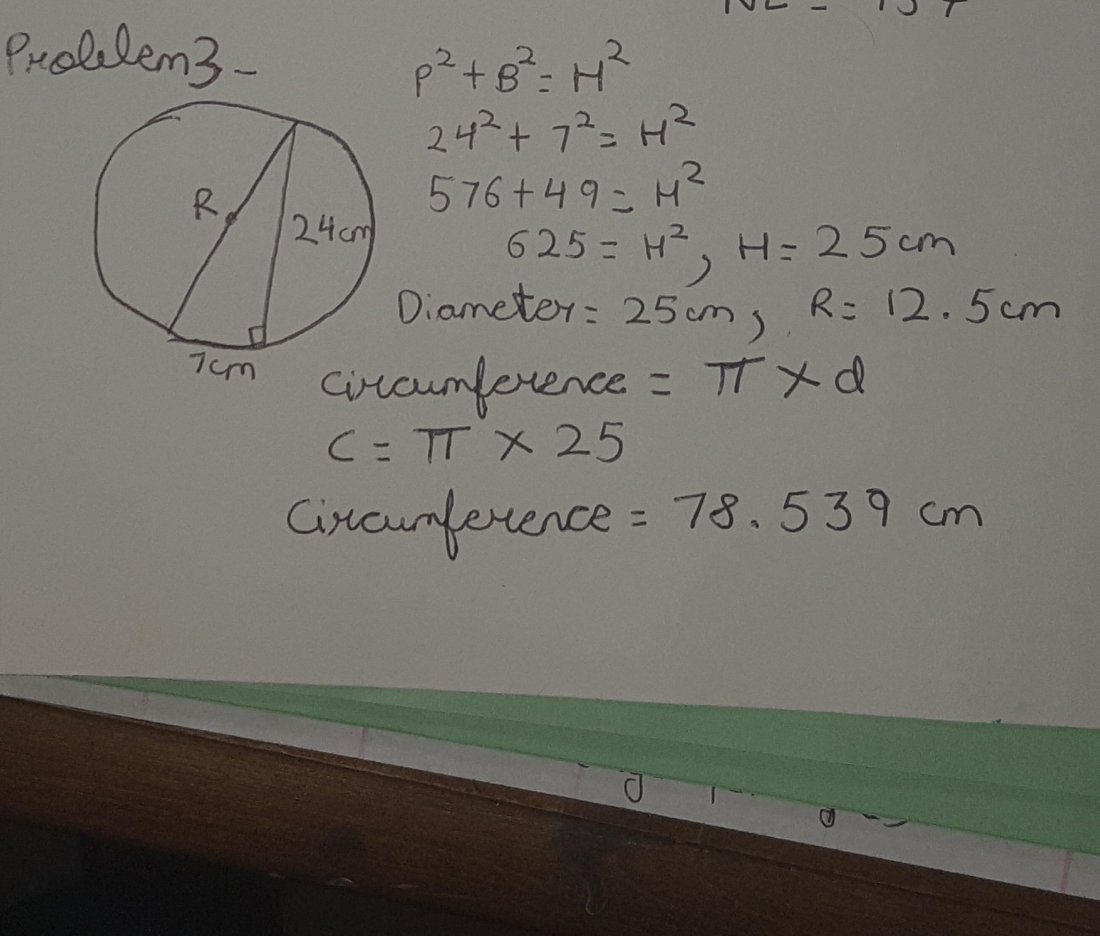


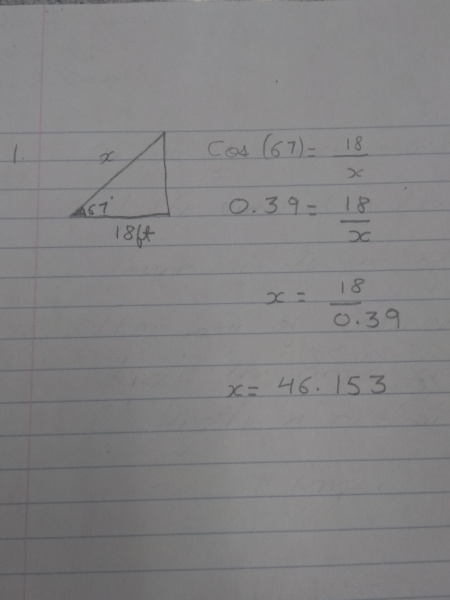





 W have been given angle A and angle C as 79.737 and 59 respectively. A+ B + C is equal to 180. Every triangle is equal to 180 degree total. So now we will plug in, 79.737+ B+ 59= 180
W have been given angle A and angle C as 79.737 and 59 respectively. A+ B + C is equal to 180. Every triangle is equal to 180 degree total. So now we will plug in, 79.737+ B+ 59= 180